L'équation de Tsiolkovski est l'équation fondamentale de l'astronautique reliant l'accroissement de vitesse au cours d'une phase de propulsion d'un astronef doté d'un moteur à réaction au rapport de sa masse initiale à sa masse finale.
On la doit à Constantin Tsiolkovski et, indépendamment, à Hermann Oberth.
Sommaire
[masquer]Énoncé[modifier | modifier le code]
L'équation de Tsiolkovski s'écrit :
où :
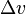 est la variation de vitesse entre le début et la fin de la phase propulsée considérée ;
est la variation de vitesse entre le début et la fin de la phase propulsée considérée ; est la vitesse d'éjection des gaz1 ;
est la vitesse d'éjection des gaz1 ; est la masse totale de l'astronef au début de la phase propulsée (indice i pour initial) ;
est la masse totale de l'astronef au début de la phase propulsée (indice i pour initial) ; est la masse totale de l'astronef à l'issue de la phase propulsée (indice f pour final), exprimée dans la même unité que
est la masse totale de l'astronef à l'issue de la phase propulsée (indice f pour final), exprimée dans la même unité que  ;
;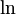 est la fonction logarithme népérien.
est la fonction logarithme népérien.
Établissement[modifier | modifier le code]
Démonstration[modifier | modifier le code]
Cette équation est établie en intégrant l'équation de conservation de la quantité de mouvement entre le début et la fin de la phase propulsée sous les hypothèses suivantes :
- l'étude du mouvement est faite dans un référentiel d'inertie ;
- l'astronef n'est soumis qu'à la force de poussée fournie par ses moteurs, aucune autre action extérieure (gravité, efforts aérodynamiques) n'est prise en compte (voir à la fin de l'article pour la prise en compte de la gravité) ;
- la vitesse d'éjection des gaz est constante.
À un instant donné, lorsque le vaisseau de masse  se déplaçant à la vitesse
se déplaçant à la vitesse  éjecte une petite quantité d'ergol à la vitesse
éjecte une petite quantité d'ergol à la vitesse  , on note
, on note 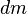 sa variation de masse2 et
sa variation de masse2 et  sa variation de vitesse. La variation de quantité de mouvement du système isolé (vaisseau + ergol éjecté) est nécessairement nulle, il vient donc :
sa variation de vitesse. La variation de quantité de mouvement du système isolé (vaisseau + ergol éjecté) est nécessairement nulle, il vient donc :
 se déplaçant à la vitesse
se déplaçant à la vitesse  éjecte une petite quantité d'ergol à la vitesse
éjecte une petite quantité d'ergol à la vitesse  , on note
, on note 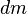 sa variation de masse2 et
sa variation de masse2 et  sa variation de vitesse. La variation de quantité de mouvement du système isolé (vaisseau + ergol éjecté) est nécessairement nulle, il vient donc :
sa variation de vitesse. La variation de quantité de mouvement du système isolé (vaisseau + ergol éjecté) est nécessairement nulle, il vient donc : .
.
Pour obtenir la variation de vitesse  de l'astronef quand sa masse passe de
de l'astronef quand sa masse passe de  à
à  , on peut intégrer cette petite variation de vitesse :
, on peut intégrer cette petite variation de vitesse :
 de l'astronef quand sa masse passe de
de l'astronef quand sa masse passe de  à
à  , on peut intégrer cette petite variation de vitesse :
, on peut intégrer cette petite variation de vitesse : .
.
Puisque  ,
,  , la variation de vitesse du vaisseau a donc comme prévu la même direction que la projection des ergols et en sens opposé.
, la variation de vitesse du vaisseau a donc comme prévu la même direction que la projection des ergols et en sens opposé.
 ,
,  , la variation de vitesse du vaisseau a donc comme prévu la même direction que la projection des ergols et en sens opposé.
, la variation de vitesse du vaisseau a donc comme prévu la même direction que la projection des ergols et en sens opposé.Commentaires[modifier | modifier le code]
Il est souvent dit que pour trouver cette équation, il faut que le débit massique d'ergol soit constant pendant la phase de propulsion ; mais ce n'est pas obligatoire, même si cela simplifie le travail d'intégration dans un premier temps.
L'équation est valable aussi bien lors d'une phase d'accélération (la poussée est dans la direction de la vitesse, 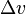 est positif : c'est un accroissement de vitesse) ou de décélération (la poussée est de direction opposée à la vitesse,
est positif : c'est un accroissement de vitesse) ou de décélération (la poussée est de direction opposée à la vitesse, 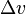 est négatif : c'est une réduction de vitesse).
est négatif : c'est une réduction de vitesse).
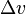 est positif : c'est un accroissement de vitesse) ou de décélération (la poussée est de direction opposée à la vitesse,
est positif : c'est un accroissement de vitesse) ou de décélération (la poussée est de direction opposée à la vitesse, 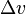 est négatif : c'est une réduction de vitesse).
est négatif : c'est une réduction de vitesse).
La différence entre la masse initiale  et la masse finale
et la masse finale  correspond à la masse que la fusée a éjectée durant sa propulsion ; on appelle cette masse éjectée la masse d'appui (« d'appui » parce que c'est la masse sur laquelle la fusée s'est appuyée pour se propulser).
correspond à la masse que la fusée a éjectée durant sa propulsion ; on appelle cette masse éjectée la masse d'appui (« d'appui » parce que c'est la masse sur laquelle la fusée s'est appuyée pour se propulser).
 et la masse finale
et la masse finale  correspond à la masse que la fusée a éjectée durant sa propulsion ; on appelle cette masse éjectée la masse d'appui (« d'appui » parce que c'est la masse sur laquelle la fusée s'est appuyée pour se propulser).
correspond à la masse que la fusée a éjectée durant sa propulsion ; on appelle cette masse éjectée la masse d'appui (« d'appui » parce que c'est la masse sur laquelle la fusée s'est appuyée pour se propulser).
La projection de masse d'appui est d'ailleurs la seule façon de se déplacer dans l'espace (même la propulsion à voile solaire se fait par modification de la quantité de mouvement du vent solaire).
Pour les fusées thermo-chimiques (Ariane, Soyouz, Navette, etc.), la masse d'appui est la masse des ergols (poudre, ou dioxygène et dihydrogène) et cette masse d'appui est également source d'énergie chimique : c'est donc la masse d'appui elle-même qui contient l'énergie qui servira à sa propre éjection.
Ce n'est plus le cas pour les moteurs ioniques (qui représentent sans doute l'avenir de la conquête spatiale). Ceux-ci sont régis tout pareillement par l'équation de Tsiolkovski, mais leur masse d'appui est constitué d'un gaz neutre (du xénon) ; c'est la très forte vitesse d'éjection de cette masse d'appui qui rend ces moteurs très économes en masse d'appui (il leur faut cependant une source d'énergie pour réaliser l'éjection). À ce titre, le fonctionnement des moteurs ioniques est comparable à celui des fusées à eau dans lesquelles l'eau n'est utilisée que pour sa masse (l'énergie résidant dans l'air comprimé).
Dans le cas où la phase propulsée est réalisée aux moyens de plusieurs étages fonctionnant successivement, la même équation de Tsiolkovski peut être utilisée pour le vol de chaque étage. On peut ainsi montrer l'intérêt de telles fusées à plusieurs étages. Voir l'exemple dans la section suivante.
Malgré l'apparente simplicité de cette équation et des hypothèses qui la sous-tendent, elle constitue une approximation utile au calcul des manœuvres de changement d'orbite, ces manœuvres étant qualifiées d'impulsionnelles, c’est-à-dire effectuées en un temps suffisamment bref pour que les hypothèses de l'équation de Tsiolkovski restent approximativement valables.

Aucun commentaire:
Enregistrer un commentaire